Просмотров: 231

Античная арифметика
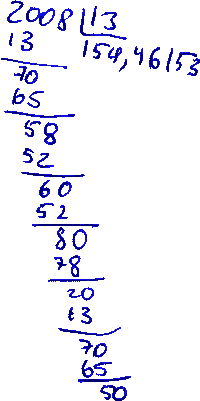
--------------------------------
MMVIII / XIII
=
?
Давай митодику, милай! (с) vvu
А, действительно, как такие вычисления делали древние римляне?
"Римляне были скрягами, вычитать и делить им и в голову не приходило.
Их задача была складывать и умножать." (с)
ЦитатаПусть требуется умножить 126 на 37 (знаки действий будем употреблять
современные; у римлян их не было, названия действий писались словами).СХХVI з XXXVII ?
Приходится умножать множимое на каждую цифру множителя отдельно, а
затем сложить все произведения.----------------------------------------------------------------------------
"Наука и жизнь", э 5, 1970
Это - абсолютная ахинея, основанная на привычном, усвоенном еще со школьной скамьи, арифметическом десятичном счете.
Не могло этого быть у древних римлян никоим образом! Мозгов бы не хватило.
С римскими цифрами (а также каталонскими, туамотскими, мумбо-юмбовскими, альфацентавровскими) можно совершать сложные арифметические действия, но только с помощью абака, где вычисления производятся полностью абстрагированно от обозначений чисел, которые, в свою очередь, необходимы исключительно для ввода данных и считывания результата.
То есть налицо полная аналогия с интерфейсом ЭВМ-человек, только очень древняя.
Со времен античности люди использовали простое и очень наглядное арифметическое вспомогательное средство, счеты - абак. Абак (от финик. Abax - доска, покрытая слоем песка для письма). Развивающаяся торговля нуждалась в более сложных расчетах и без вспомогательных средств уже обойтись было невозможно. Сначала использовали нарисованные в песке линии, на которые клали маленькие камешки (lat. calculi, отсюда, между прочим, и калькулятор), раковины или деревянные палочки. Потом перешли на деревянные доски или же большие плоские камни. Так возникли первые счеты, на которых производился т.н. линейный счет.

Линейным счетом, который базируется на древнеримской цифровой системе пользовались столетиями, вплоть до недавнего времени, несмотря на переход на арабские числа и позиционную систему счисления. Даже знаменитый математик Лейбниц предпочитал производить вычисления линейным счетом.
Для расчетов с покупателями торговцы на рынках использовали специальные счеты с щелями вместо линий, а то и просто столешницы или платки с нарисованными горизонтальными линиями. Нижняя линия представляет из себя единицы, следующая пятерки, потом десятки, пятидесятки, и так далее.

В щели счетов или на линии торговцы распределяли жетоны (монетки и т.п.) таким образом: два жетона в линии единиц и жетон в линии для пятерок представляют, к примеру, число 7.
Если складывают 2 и 4, то получают первоначально 6 жетонов на линии единиц. Но там, однако, есть место только для 4. Поэтому отнимают 5 жетонов и кладут вместо этого жетон на линию выше, которая стоит для числа 5. Результат выглядит как 5+1=6.
Другой пример: 5+5+5 - это соответствует 3 жетонам на линии 5. Но на ней допускается, однако, только один. Поэтому отнимают 2 и кладут жетон на линию 10. Результат 5+10=15.
Дети учат таблицу умножения сегодня уже в первом классе, а тогда школьникам жилось гораздо легче, чем сейчас. Таблицу умножения им нужно было учить только до четырех. Но легче им жилось еще и по другой причине. До 17-ого века математика (арифметика) совсем отсутствовала в учебных программах т.н. латинских школ. Простой народ относился к тем, кто умел оперировать с числами большими, чем пальцев на руке, и даже совершать с ними арифметические действия как к колдунам. Даже студенты европейских университетов воспринимали арифметику с подозрением.
Арифметическому ликбезу в широких слоях населения Германия обязана математику Адаму Рис - Adam Ries (ошибочно называемого по-русски Адам Ризе), выпустившему в начале 16-го века несколько книг на немецком языке, посвященных арифметике и, в том числе, простому счету на линиях.
Этим счетом от Адама Риса из его книги Rechnung auff der linihen (1518), с примерами выполнения операций сложения, вычитания, но также умножения и деления, я и хочу здесь поделиться......
Конструкция счетов
На счетах находятся минимум четыре горизонтальные линии, со значением снизу вверх 1, 10, 100 и 1000. Для предотвращения путаницы на линии "тысячи" нанесен крест. Области между линиями называются "spacium" или "spacio" и соответствуют значениям 5, 50 и 500. Как правило, на абаке имеются две вертикальные линии, которые делят счеты на т.н. "bancire" и служат для отделения чисел друг от друга.

Выкладывание числа (Numeratio)
Число выкладывается на счетах жетонами. Два жетона на линии единиц означают число 2, если оба жетона лежат на линии десятков, то они представляют число 20. Если жетон кладется теперь дополнительно в пятисотый spacium, то получают число 520.
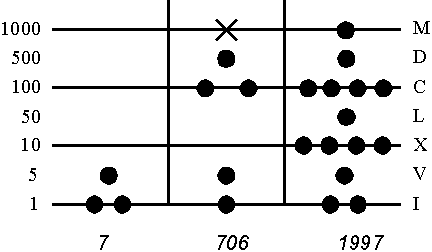
Арифметические правила - Elevatio и Resolvatio
Elevatio - это перемещение жетонов в следующий более высокий разряд с одновременным их сложением (связка).
Перемещение с линии:
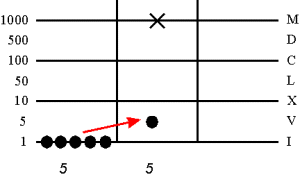
Перемещение из Spacio:
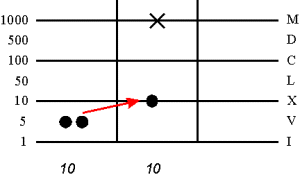
Resolvatio - обратный предыдущему действию процесс (разложение).
Разложение (перемещение вниз) с линии:
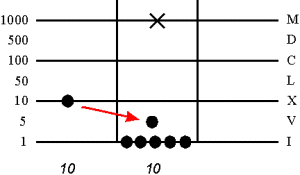
Разложение (перемещение вниз) из Spacio:
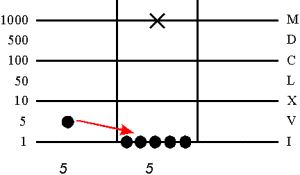
Сложение
Сложение двух чисел производится в четыре действия и показывается здесь на примере сложения 194 и 76.
1. Numeratio
Выкладываются оба числа в двух смежных столбцах - Bankier'ах
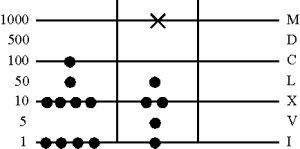
2. Сложение
Простое сдвижение жетонов вместе по разрядам в одном столбце
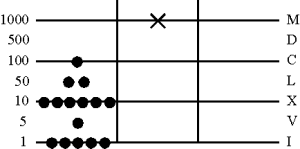
3. Elevatio
Перемещение жетонов на разряд выше с их сложением, если на одной линии оказываются больше четырех, а в Spacio более одного жетона
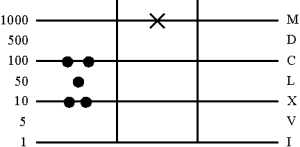
4. Считываем результат
194 + 76 = 270
Вычитание
Вычитание двух чисел производится аналогично сложению. Разумеется, может случиться, что достаточное количество жетонов на линии или в Spacio не имеется в наличии. В этом случае жетоны на более высоких линиях или Spacio должны быть подвержены разложению.
Пример 1. (Без разложения): 287 - 21 = ?
1. Numeratio
Раскладка жетонов в первом столбце.
Прим.: Вычитаемое, для наглядности, выкладывается во втором столбце
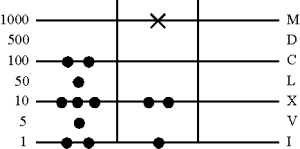
2. Вычитание
Удаление вычтеных жетонов из соответствующих разрядов.
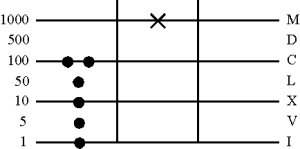
3. Считываем результат
287 - 21 = 266
Пример 2 (с разложением): 287 - 43 = ?
1. Numeratio
Раскладка жетонов в первом столбце.
Прим.: Вычитаемое, для наглядности, выкладывается во втором столбце
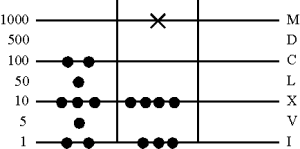
2. Разложение
Производится жетонами из Spacio на линии нижележащего разряда
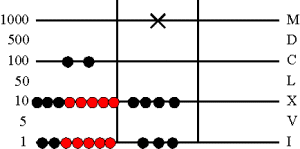
3. Вычитание
Удаление вычтеных жетонов из соответствующих разрядов.
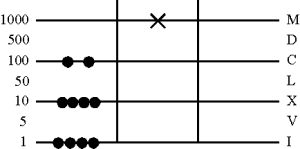
Умножение
Умножение двух чисел основывается на многократном сложении по частям. Используют в этом процессе все возможные арифметические преимущества. Умножение на 10, например, означает, что расположенные на линии или в Spacio жетоны перемещаются на одну строку наверх соответственно в десятичные, сотенные или тысячные разряды.
Пример 1: 38 * 123 =?
1. Numeratio
Раскладка жетонов первого множителя в первом столбце.
Прим.: Такой же, для наглядности, выкладывается во втором столбце
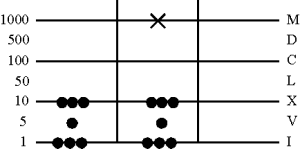
2. Сначала умножают 38 на 100
Жетоны перемещаются на две строки кверху
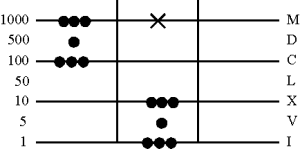
3. Умножение 38 на 20
Число жетонов во втором столбце удваивается (38+38) и перемещается на одну строку вверх (76х10) и все это приплюсовывается к жетонам первого столбца

4. Умножение 38 на 3
Число 38 выкладывается три раза и просто суммируется с жетонами первого столбца.

5. Elevatio (наведение порядка в разрядах) и считывание результата
38 * 123 = 4674

Деление
Деление Адам Рис производит вычитанием, то есть многократным вычитанием делителя из делимого. При этом количество вычитаний отмечается в банкире и представляет собой в конечном итоге результат. Возьмем простой пример (9: 3 =?):
1. Numeratio
Раскладывается делимое, делитель "в уме"

2. Вычитание трех жетонов
Три жетона удаляются из делимого и один жетон помещается на линию единиц в крайнем правом столбце

3. Resolutio
Разложение пятерки на линии единичных разрядов, чтобы можно было произвести очередные вычитания
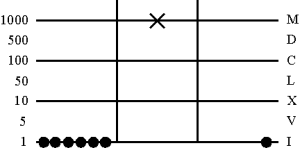
4. Считываем результат
В третьем столбце - результат деления. Если при делении получается остаток, то его размещают на верхней линии абака.
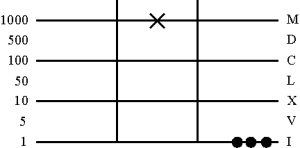
При делении двух- и более значных чисел деление аналогично процессу умножения, то есть стараются через многократное разложение как можно раньше вычесть делитель.
Например (276 : 23 = ?):
1. Numeratio
Раскладывается делимое, делитель "в уме"
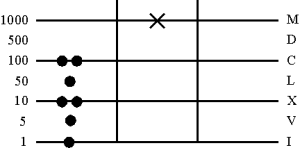
2. Resolutio пятидесятного Spacio
Раскладывается разряд пятидесяток, чтобы можно было вычесть 230
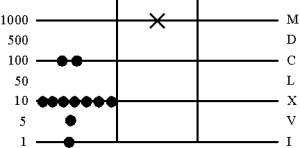
3. Вычитание 230
При вычитании из делимого вычитается десятикратное значение делителя!
Таким образом жетон кратности укладывается на линии десятков.
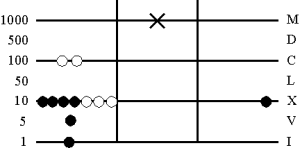
4. Resolutio пятиричного Spacio и вычитание 23 (два раза по 23).

5. Считываем результат
276 : 23 = 12
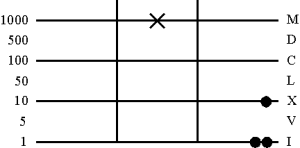
Уфффф...!
Кстати, здесь под жетонами подразумеваются calculi. Пользоваться в абаке можно чем угодно: жетонами, монетами, камешками, чопиками, даже наперстками.
А вот теперь возвращаемся к нашим баранам.
Попробуем решить поставленную vvu задачу и разделить древним линейным способом 2008 на 13 или, говоря по-нашему по-античному,
MMVIII / XIII = ?
По методике Адама Риса, а вернее по существовавшей в его время счетной практике, раскладываем камешками-calculi число 2008 на абаке следующим образом:
Причем нам, в принципе, неважно ориентируемся ли мы по арабским цифрам (слева), неизвестным античности или же по римским (справа). Наши calculi легко находят свои места - MM-V-III
С этого момента мы, как и положено нерадивым ленивым недорослям-патрициям, вообще забываем о том, что у чисел существуют какие-либо буквенно-иероглифические изображения (нам они ни к чему, только отвлекают) и концентрируемся исключительно на камешках-calculi и их количестве на абаке.
Зная о том, что 2000 - это 20 раз по 100, мы выкладываем 20 камешков на сотенной линии. Теперь, согласно правилу, мы приводим десятичную размерность делителя (13) к десятичной размерности делимого, чтобы разместить их на одной линии и осуществить действие вычитания, т.е. в нашем случае считаем не 13, а 13 сотен. Вычитаем 20с - 13с = 1раз и 7с в остатке, где с - как хотите, сотни или они же calculi.
Этот 1 раз мы замечаем камешком на линии сотен в правом секторе-столбце абака
От остатка в 7с мы уже не можем отнять еще раз 13с, поэтому разлагаем эти сотни на десятки, для чего нам придется вывалить в кучку целых семьдесят камешков на линии десятков.
От 70д камушек мы можем отнять по 13д камушек целых 5 раз, что и отмечаем на соответствующей линеечке с правой стороны пятью камушками. В невычитаемом остатке у нас остаются 5д камушек или же 50. А вместе с почти забытыми восемью камушками, сиротливо лежащими все это время на нижних разрядах абака, и все 58.
Последнее наше действо уж и совсем простое. Нам остается отнять от 58 камешков 4 раза по 13, больше не отнимается. Что и отмечаем в разряде единиц.
Нам остается теперь считать с абака наш результат, снимая с него камушки. И только теперь мы вспоминаем, что числа имеют какие-то обозначения!!!
C-XXXXX-IIII или же по новому стилю - CLIV
А на абаке у нас осталось 6 камешков, которые никак на 13 не делятся.
Не думаю, что римляне записали бы этот остаток, как 6/13 или VI/XIII.
Дробей римляне избегали так же упорно, как и больших чисел. В практических задачах, связанных с измерениями, они не использовали дроби, подразделяя единицу измерения обычно на 12 частей, с тем чтобы результат измерения представить в виде составного числа, суммы кратных различных единиц, как это делается сегодня, когда длину выражают в ярдах, футах и дюймах. Английские слова «ounce» (унция) и «inch» (дюйм) происходят от латинского слова uncia (унция), обозначавшего одну двенадцатую основной единицы длины.
Например, римлянин мог сказать, что он прошел семь унций пути или прочел пять унций книги. При этом, конечно, речь не шла о взвешивании пути или книги. Имелось в виду, что пройдено 7/12 пути или прочтено 5/12 книги. -
Поэтому они, скорее всего, записали бы результат вычисления MMVIII / XIII =
как CXXXXXIIII и VI унций, что очень близко к 6/13. А, и так сойдет! Не стрелять же из этого...
Какой можно сделать из всего этого вывод?
Да, древние могли производить арифметические действия, пользуясь неудобными буквенно-символическими обозначениями чисел, в частности такими, как римские цифры. Но только в определенных пределах они могли это делать на пальцах, в уме, да и то только складывать и вычитать. Для арифметических действий с двух- и более значными цифрами, а так же для осуществления операций умножения и деления им необходимы были примитивные счеты - абак. Как мы видели это работает без всякой оглядки на сложную и громоздкую систему записи римскими цифрами. В процессе вычислений они и вовсе не нужны, а нужны лишь для записи конечного результата. Чем и пользовались. От торговца до архитектора. Начертил палкой на песке, здесь и сейчас, свой абак, нагреб в ладони гальку и сиди, себе, считай.
Без абака - ты собака, а с абаком - человек (с)
P.S.
Я попытался разобраться с проблемой счета римскими цифрами древними.
А ведь они как-то считали, не правда ли? И нашел, что это возможно, но только при помощи абака, прообраза привычных нам счетов. Еще я пришел к выводу, что, пользуясь абаком, нет никакой необходимости забивать себе и людям голову римскими цифробуквами, которые нужны лишь в момент "ввода" и "вывода данных на печать". В принципе, они могут быть записаны и иероглифами и плящущими человечками.
Более того, я подозреваю, что почти непозиционная римская пятиричная система счисления предопределила плавный безреволюционный переход к позиционной десятичной.
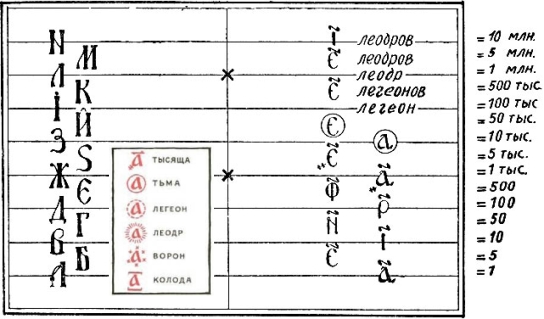
Не знаю, существует ли официально такое понятие как пятиричная система, но для меня римская так и выглядит. В ней, в отличие от еврейской, греческой, славянской и т.п., буквенных систем буквами отмечались только значения кратные 5 (10).
V — 5,
X — 10,
L — 50,
C — 100,
D — 500,
M — 1000
Эти цифробуквы и нашли свое отражение на абаке. Справочно, для наглядности.
Все остальные промежуточные числа выражались "счетными палочками" - I.
Римская система интуитивна и явно берет свое начало в счете на пальцах, где после четырех предъявленных покупателю/продавцу пальцев следует пять, она же - "пядь" - символическая V, а после предъявления следующих четырех - "две пяди" V V или Х.
Семь пядей во лбу, таким образом, выражается римскими цифрами как ХХХV
P.P.S.
А как считали на Руси до введения арабских цифр? Да так же!